Типы данных для выполнения матричных преобразований

      В библиотеке Managed DirectX 9 имеются уже реализованные и удобные в использовании типы данных для работы с матрицами и векторами. Эти типы имеют удобные и быстрые методы выполнения векторных и матричных операций. Поэтому, в данном случае, нет необходимости создавать какие-либо свои типы данных, а нужно использовать уже имеющиеся. Далее я приведу краткое описание этих типов.

      Структуры векторов:

• Двумерные вектора – структура Vector2:
  Vector2 pV2 = new Vector2(float X, float Y); – конструктор создания 2D вектора;
• Трёхмерные вектора – структура Vector3:
  Vector3 pv3 = new Vector3(float X, float Y, float Z); – создание 3D вектора;
• Трёхмерные вектора в однородных координатах – структура Vector4:
  Vector4 pv4 = new Vector4(float X, float Y, float Z, float W); – создание 4D вектора;

      Вектора имеют поля, через которые можно обращаться к компонентам вектора: X, Y, Z, W. Вне зависимости от того, какого типа вектор, он имеет общие для всех векторов методы. Многие методы имеют как обычную, так и статическую реализацию. Я приведу лишь названия основных статических методов, без указания типов передаваемых в качестве параметров векторов:

• Vector Vector::Add(pVa, pVb); – сложение двух векторов: pVa + pVb;
• Vector Vector::Subtract(pVa, pVb); – вычитание двух векторов: pVa - pVb;
• Vector Vector::Scale(pV, float K); – умножение вектора на число: pV·K;
• Vector4 Vector::Transform(pV, Matrix M); – умножение вектора на матрицу: pV·M;
• Vector Vector::Normalize( pV ); – нормализация вектора: pV/|pV|;
• Vector Vector::Cross(pVa, pVb); – векторное произведение векторов: [pVa x pVb];
• float Vector::Dot(pVa, pVb); – скалярное произведение векторов: (pVa·pVb);
• float Vector::Length( pV ); v вычисление длины (нормы) вектора: |pV|;

      Структура матрицы:

      Matrix pM = new Matrix( ); – конструктор создания 0-й матрицы размерности 4x4;

      Доступ к компонентам матрицы осуществляется через поля именуемые как Mij, где i=1..4, j=1..4. В структуре матрицы так же определены статические методы, позволяющие создавать матрицы, выполняющие стандартные пространственные аффинные преобразования:

• Matrix pM = Matrix::Translation(float Tx, float Ty, float Tz); – создание матрицы, выполняющей преобразование смещения на вектор (Tx, Ty, Tz);
• Matrix pM = Matrix::RotationX[Y,Z]( float Angle ); – создание матрицы, выполняющей преобразование поворота вокруг оси X (Y или Z) на угол Angle (в рад.);
• Matrix pM = Matrix::RotationAxis( Vector pVAxis, float Angle); – создание матрицы, выполняющей преобразование поворота вокруг оси pVAxis на угол Angle (в рад.);
• Matrix pM = Matrix::Scaling( float Sx, float Sy, float Sz); – создание матрицы, выполняющей преобразование масштабирования на скалярные велисины (Sx, Sy, Sz);

      Как и для вектора, в структуре матрицы реализованы статические и нестатические методы, выполняющие основные операции над матрицами. Приведу лишь некоторые из статических реализаций этих методов:

• Matrix Matrix::Add( pMl, pMr); – сложение двух матриц: pMl+pMr;
• Matrix Matrix::Multiply( pMl, pMr); – умножение двух матриц: pMl·pMr;
• Matrix Matrix::Invert( pM ); – вычисление обратной матрицы: pM^-1;
• Matrix Matrix::TransposeMatrix( pM ); – транспонирование матрицы: pM^T;

       Пространственные и проекционные системы координат

      Системы координат в DirectX описываются матрицами Matrix. В зависимости от использования, системы координат принято называть по разному.

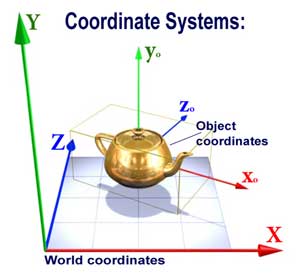
Исходную систему координат, по отношению к которой выполняются все преобразования объектов сцены, принято называть мировой системой координат.

Систему координат, связанную с некоторым объектом, и преобразуемую вместе с объектом, называют объектовой системой координат (говорят, что объект “вморожен” в систему координат).

      Для изменения мировой системы координат в DirectX, необходимо изменить определяющую её матрицу. Матрица мировой системы координат хранится в поле объекта Device – устройства, выполняющего все графические операции Direct3D:

Device→Transform→World;

      Если мировая система координат (X, Y, Z) преобразована к (Xo, Yo, Zo), то все объекты будут отображаться в новой объектовой системе координат (см. рис.).

      Кроме пространственных систем координат, в DirectX есть так же проекционные системы координат, которые используются в процессе рендеринга сцены – т.е. при проецировании 3-х мерных объектов на плоскость камеры. Положение и направление камеры определяются матрицей вида:

device→Transform→View;

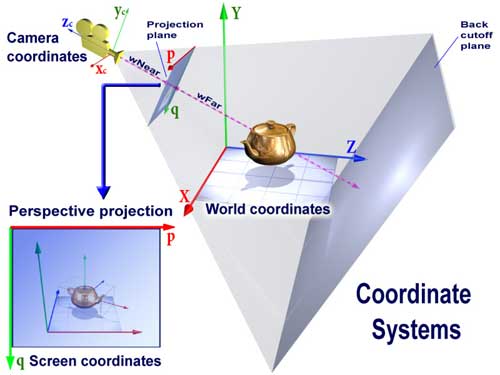
Таким образом, матрица вида определяет положение и ориентацию системы координат камеры (Xc, Yc, Zc) (см. рис. ниже - Camera coordinates).

Матрица вида может быть автоматически сформирована путём вызова статического метода LookAtLH по передаваемым векторам положения камеры (CamPosition), точки фокуса (camTarget) и верха камеры (CamUpVector):

device→Transform→View = Matrix::LookAtLH( Vector3 camPosition, Vector3 camTarget, Vector3 camUpVector );

      Кроме того, для полного определения процесса проецирования, нужно задать параметры используемой нами камеры. Эти параметры хранятся в матрице проецирования:

device→Transform→Projection;

      Прежде всего, необходимо определить какой тип проекции будет использоваться:

• Перспективная проекция – используется для описания сцены, представленной в виде усечённой пирамиды (frustrum), где внутренняя часть пирамиды является просматриваемой областью нашей сцены (см. рис. 2.13). В перспективной проекции все лучи зрения пересекаются в точке расположения камеры. Матрица перспективной проекции создаётся методом PerspectiveFovLH:

  device→Transform→Projection = Matrix::PerspectiveFovLH( float viewAngle, float aspectRation, float znearPlane, float zfarPlane );

  Два параметра в этой функции – ближняя и дальняя плоскости (znearPlane, zfarPlane) описывают пределы этой пирамиды, причём дальняя плоскость является основанием, а ближняя плоскость проходит по месту отсечения вершины пирамиды. Поле зрения камеры определяется углом раствора камеры (viewAngle) и форматным соотношением (aspectRatio) сторон плоскостей усечения пирамиды видимого объёма.
• Ортогональная проекция – используется для описания сцены, представленной в виде параллелепипеда, внутренняя часть которого является просматриваемой областью сцены. В ортогональной проекции все лучи параллельны оси зрения камеры. Матрица ортогональной проекции задаётся методом OrthoLH:

  device→Transform→Projection = Matrix::OrthoLH( float width, float height, float znearPlane, float zfarPlane );

  В функцию передаются два параметра, определяющие расстояние от камеры до ближней и дальней плоскостей отсечения (znearPlane, zfarPlane). Другие два параметры определяют поле зрения камеры – высоту и ширину сторон параллелепипеда (width, height).

Когда сцена спроецирована на проекционную плоскость, то координаты точек этой плоскости измеряются в экранных координатах (p, q) (Screen Coordinates).

       Материалы, текстуры и загрузка полигональных моделей из X-файла

      Для моделирования реалистичных геометрических сцен, в качестве составных объектов используются полигональные модели или Mesh-объекты.

Полигональной моделью (Mesh) называется объект, содержащий вершинный и индексный буферы, определяющих полигоны некоторого геометрического объекта.

      Основным преимуществом использования Mesh-объектов является возможность удобного хранения и формирования сложных геометрических объектов, а также их эффективный рендеринг.

      Для реалистичного отображения не достаточно только информации о его вершинах. К примеру, Mesh-объекты не содержат информации о цвете вершин, а так же способе наложения на объект текстуры, более подробно описывающеё его поверхность.

Материал – это описание, того каким образом покрываемая им поверхность будет отражать свет. Материал включает в себя отражаемый диффузный (Diffuse) и общий цвет (Ambient), цвет блика (Speccular), параметры отражения света и уровень прозрачности материала (Alpha).

Текстура – это изображение, которое накладывается на поверхность геометрического объекта определённым образом. Способ наложения текстуры определяют текстурные координаты.

      Информация о текстурных координатах обычно добавляется в буфер вершин геометрического объекта, на который будет наложена текстура. Обычно задание текстурных координат (и буфера вершин в целом) достаточно трудоёмкий процесс для сложных объектов. Но, к счастью, вся информация о полигональной модели может быть загружена из файла специального формата – X-файла.

X-файл – это файл в формате XML, хранящий следующие данные полигональной модели:

• Подобъекты полигональной модели;
• Буферы вершин (с координатами текстуры) каждого из подобъектов;
• Индексные буферы каждого из подобъектов;
• Параметры материалов каждого из подобъектов;
• Информацию о файле текстуры каждого из подобъектов.

      Данные из X-файла могут быть загружены с помощью следующей функции:

// Код функции приведён на языке C++/CLI:
Mesh^            MyMesh;      // Внешнее поле для меш-объекта
array‹Material›^ MyMaterials; // Внешний массив материалов модели
array‹Texture^›^ MyTextures;  // Внешний массив текстур модели

void LoadMesh( String^ file )
{
  array‹ExtendedMaterial›^ mtrl;
  // Загружаем модель из X-файла:
  MyMesh = Mesh::FromFile(file, MeshFlags::Managed, device, mtrl);

  // Если модель содержит материалы, сохраняем их:
  if ((mtrl != nullptr) && (mtrl->Length > 0))
  {
    MyMaterials = gcnew array‹Material›( mtrl->Length );
    MyTextures  = gcnew array‹Texture^›( mtrl->Length );
    // Сохраняем каждый материал и текстуру:
    for (int i=0; i < mtrl->Length; i++)
    {
      MyMaterials[i] = mtrl[i].Material3D;
      if ( (mtrl[i].TextureFilename != nullptr) &&
           (mtrl[i].TextureFilename != String::Empty) )
      {// Если есть информация о текстуре - пробуем загрузить её:
        MyTextures[i] = TextureLoader::FromFile(device,
                        mtrl[i].TextureFilename);
      }
    }
  }
}

Перейти к следующему разделу