Существуют общие закономерности в структуре (строении) самых различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул механизмов.

Под числом степеней подвижности механизма (обозначение W) будем понимать число независимых параметров, определяющих положение всех подвижных звеньев механизма.

      Такими параметрами являются независимые координаты, определяющие положения входных звеньев. Очевидно, число степеней подвижности будет равно числу всех входных звеньев.

      Для пространственных механизмов в настоящее время наиболее распространена формула Малышева, вывод которой производится следующим образом.

      Введём обозначения следующих числовых величин:

• m – число звеньев (включая стойку);
• p1, p2, p3, p4, p5 – число одно-, двух-, трёх-, четырёх- и пятиподвижных пар;
• n=m-1 – число подвижных звеньев механизма.

      Если бы все подвижные звенья были свободными телами, общее число степеней свободы было бы равно 6n. Однако каждая одноподвижная пара V-го класса, накладывает на относительное движение звеньев, образующих пару 5 связей, каждая двухподвижная пара IV-го класса – 4 связи и т. д. Следовательно, общее число степеней свободы, равное шести, будет уменьшено на величину:

(2.1)

      В общее число наложенных связей может войти некоторое число q избыточных (повторных) связей, которые дублируют другие связи, не уменьшая подвижности механизма, а только обращая его в статически неопределимую систему [1]. Поэтому число степеней свободы пространственного механизма, равное числу степеней свободы его подвижной кинематической цепи относительно стойки, определяется по следующей формуле Малышева:

(2.2)

      При q=0 механизм – статически определимая система, при q>0 – статически неопределимая система. В частном случае, если число степеней подвижности механизма W найдено из геометрических соображений, то из формулы (2.2) можно найти число избыточных связей q и решить вопрос о статической определимости механизма. Или же, зная, что механизм статически определимый можно найти W.

      Если избыточных связей нет (q=0), сборка механизма происходит без деформирования звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися [1]. Если избыточные связи есть, то сборка механизма и движение его звеньев становится возможным только при деформировании последних.

      Для плоских механизмов без избыточных связей структурная формула носит имя П. Л. Чебышева, впервые предложившего её в 1869 году для рычажных механизмов с вращательными парами и одной степенью свободы. В настоящее время формула Чебышева распространена на любые плоские механизмы и выводится с учётом избыточных связей следующим образом.

      Пусть в плоском механизме, имеющем m звеньев (включая стойку), n=m-1 – число подвижных звеньев, p_н – число низших пар и p_в – число высших пар. Если бы все подвижные звенья были свободными телами, совершающими плоское движение, общее число степеней свободы было бы равно 3n. Однако каждая низшая пара накладывает на относительное движение звеньев, образующих пару, две связи, а каждая высшая пара накладывает одну связь, оставляя 2 степени свободы.

      В число наложенных связей может войти некоторое число q_п избыточных (повторных) связей, устранение которых не увеличивает подвижности механизма. Следовательно, число степеней свободы плоского механизма, т.е. число степеней свободы его подвижной кинематической цепи, относительно стойки, определяется по следующей формуле Чебышева:

(2.3)

      Индекс “П” напоминает о том, что речь идёт об идеально плоском механизме, или, точнее, о его плоской схеме, поскольку за счёт неточностей изготовления плоский механизм в какой-то мере является пространственным.

      По формулам (2.2), (2.3) проводят структурный анализ имеющихся механизмов и синтез структурных схем новых механизмов.

Пассивной связью можно назвать дополнительное звено, которое не накладывает ограничений на движение механизма. Обычно она вводится для увеличения жёсткости механизма или перевода механизма через особые положения, в которых наблюдается неопределенность движения звеньев.

      В так называемом “механизме параллельных кривошипов” (рис. снизу а) звено 3 может изменить направление вращения при неизменном направлении вращения ведущего звена 1, когда механизм приходит в горизонтальное положение. Для того, чтобы этого избежать, в состав механизма включают дополнительное звено 4.

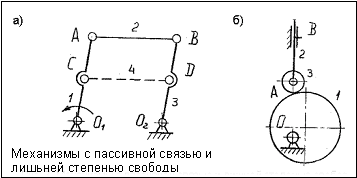
      При структурном анализе механизма пассивные связи не учитывают. Если по формуле степень подвижности механизма будет равна нулю, но заранее известно, что рассматриваемая цепь подвижна, то следует искать пассивные связи.

      Наоборот, когда в механизм вводятся дополнительные звенья, имеющие собственную свободу движения, тогда говорят о лишней степени свободы. Так, степень подвижности кулачкового механизма (рис. сверху, б) W=2 (n=3, p1=3, p2=1). Построив заменяющий механизм, нетрудно убедиться, что он имеет степень подвижности W=1. Лишнюю степень подвижности для кулачкового механизма вносит свободный поворот ролика вокруг оси вращения без влияния на характер движения механизма в целом.

Перейти к следующему разделу