Впервые закон образования механизмов был сформулирован в 1914 г. русским ученым Леонидом Владимировичем Ассуром применительно к плоским шарнирным механизмам и затем позднее распространен на другие механизмы И. И. Артоболевским. Закон образования механизмов можно сформулировать следующим образом:

Закон Ассура: Всякий механизм представляет собою совокупность одного или нескольких, двухзвенных (первичных) механизмов и одной или нескольких групп нулевой подвижности.

      Группы нулевой подвижности не изменяют числа степеней подвижности двухзвенных механизмов. В связи с этим сформулированный закон позволяет без помощи структурной формулы определить число степеней подвижности любого механизма.

      Закон Асура является первостепенно важным для решения задач моделирования пространственных механизмов. Этот закон даёт простой алгоритм решения задачи синтеза произвольного механизма и методику анализа имеющегося механизма (см. рис. снизу).

Двухзвенный (первичный) механизм состоит из подвижного звена и стойки, образующих обратимую пару.

      Двухзвенные простейшие механизмы (т. е. механизмы, имеющие пару пятого класса) широко применяются в технике, например, в турбинах, электродвигателях, генераторах, воздуходувках и т. п.

      Как следует из сформулированного закона Ассура, двухзвенный механизм представляет собою основу многозвенного механизма. Если двухзвенный механизм является простейшим, то в этом случае подвижное звено является входным звеном образуемого механизма.

      Очевидно, одна и та же стойка может одновременно входить в состав нескольких таких двухзвенных, не зависящих друг от друга механизмов. Подвижные звенья этих механизмов представляют собою не что иное, как начальные звенья, причем каждое из них всегда будет иметь одну степень подвижности.

Структурной группой Ассура (или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (Wгр = 0).

Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками.

     Группы могут быть различной степени сложности. В зависимости от сложности, структурные группы Ассура делятся на классы, а классы в свою очередь делятся на порядки.

Классом структурной группы Ассура называется число кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами группы (И.И. Артоболевского).

Порядок группы определяется числом внешних элементов кинематических пар, которыми группа присоединяется к имеющемуся механизму: первая группа присоединяется к первичному механизму, каждая последующая – к полученному механизму (при этом нельзя присоединять группы к одному звену).

      Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп.

      Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 1-го класса 2-го порядка. Число разновидностей таких групп для плоских механизмов с низшими парами невелико - их всего пять (см. рис. снизу).

      При структурном синтезе механизма по Ассуру (рис. вверху страницы) к выбранным первичным механизмам с заданной подвижностью W0 последовательно присоединяются структурные группы c нулевой подвижностью. Полученный таким образом механизм обладает рациональной структурой, т.е. не содержит избыточных связей и подвижностей.

      Структурному анализу по Ассуру можно подвергать только механизмы, не содержащие избыточных связей и подвижностей. Поэтому перед проведением структурного анализа необходимо устранить избыточные связи и выявить местные подвижности. Затем необходимо выбрать первичные механизмы и, начиная со звеньев наиболее удаленных от первичных, выделять из состава механизма структурные группы нулевой подвижности (рис. вверху страницы). При этом необходимо следить, чтобы звенья, остающиеся в механизме, не теряли связи с первичными механизмами.

      Ассур разработал структурную классификацию для плоских рычажных шарнирных механизмов (т.е. для механизмов только с вращательными парами). В дальнейшем Артоболевский И.И. усовершенствовал и дополнил эту классификацию, распространив ее на плоские механизмы и с поступательными парами. При этом были изменены и принципы классификации. В плоских механизмах группами являются кинематические цепи с низшими парами, которые удовлетворяют следующему условию:

(2.4)

      Решения этого уравнения в целых числах определяют параметры групп Ассура.

Таблица 2: Классификация структурных групп Ассура II-VI классов

Группа	Порядок
	2-й	3-й	4-й	5-й
II класса		—	—	—
III класса	—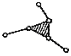
IV класса			—	—
V класса	—			—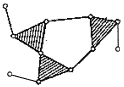
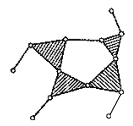VI класса	—			—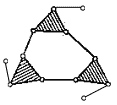

      Структурные группы 2-го класса (обычно называемые двухповодковыми группами Ассура) дополнительно классифицируются по видам, различающихся сочетанием вращательных и поступательных пар (рис. ниже):

      Структурный анализ механизма проводится путем расчленения его на структурные группы и первичные механизмы в порядке, обратном образованию механизма.